本篇将会讨论一些混音中常用效果器的实现,包括均衡器,失真器,压缩器,限制器,延迟器与混响器。
均衡器(Equalizer)
上一篇中我们实现了一个简单的低通滤波器。实际混音中使用的均衡器功能要复杂的多,并不是简单地保留一部分频率或者消去一部分频率,更多时候需要调整不同频段的相对强度和比例,类似于下图这样:

均衡器(equalizer),简称EQ,通过多个基本滤波器的串联和并联来实现对不同频段的强度调整。
组成均衡器的常用滤波器类型有低通滤波器(允许低频通过),高通滤波器(允许高频),带通滤波器(允许特定频率范围),带阻滤波器(阻止特定频率通过),钟形滤波器(增强或减弱特定频率范围)等。
例如使用均衡器制作电话音效果时,需要在均衡器里同时开启高切(低通)和低切(高通),这实质上就是让信号先通过一个低通滤波器,再通过一个高通滤波器,即串联结构。高通滤波器的递推公式推导过程同低通滤波器,根据下图的模拟电路计算传递函数再离散化即可。

高通频率响应长这样:

钟形滤波器频率响应如下,蓝色为振幅响应,品红色为相位响应:

滤波器的并联也很好理解。将一部分信号通过低通滤波器,一部分信号不作任何处理,再将两部分信号混合。理论上,我们应该得到这样的响应,即高频被衰减了一部分:

但这样做有一个严重的问题:相位差。让我们复习一下RC低通滤波电路的网络函数:
$H(jw)=\frac{1}{1+\frac{\omega}{\omega_{c}}}$
此前我们仅取模得到了振幅的变化。现在我们计算一下相位变化:
$\theta(\omega)=-arctan(\frac{\omega}{\omega_{c}})$
可以看到,信号在通过滤波器后发生了相位偏移,且此偏移是非线性的,不同频率的信号偏移程度不同。如果直接将偏移了相位的信号与原信号叠加,两者会干涉导致振幅减小。如下图:

这里$y_3=y_1+y_2 $的振幅是小于$y_1$和$y_2$的振幅之和的。
因此叠加前需要对原信号施加相同的相位改变。通常的做法是通过一个全通滤波器,即只改变相位,不改变振幅的滤波器。全通滤波器的传递函数可以是这样的:
$H(j\omega) = \frac{ j\omega – \omega_c }{ j\omega + \omega_c }$
计算一下相位:
$\theta(\omega)=-2arctan(\frac{\omega}{\omega_{c}})$
以给定滤波器的相位响应和频域不变为条件,可以求解出给定滤波器对应的全通滤波器。
在频域不变的情况下,全通滤波器实现了同样非线性的相位偏移。当滤波器并联时,我们经常需要通过相应的全通滤波器来先统一信号相位,再进行叠加。
注:这种不断迭代的滤波器属于无限冲激响应(infinite impulse response filter,IIR)型滤波器,每一时刻输出都取决于所有过往时刻。在数字滤波器一节的开头被我们弃用的滤波方案,即傅里叶变换+频域操作+傅里叶逆变换属于有限冲激响应(finite impulse response filter,FIR)型滤波器。FIR滤波器不会产生非线性的相位偏移,因此常用于对相位要求高、滤波器性能要求低的场合,比如图像处理。
失真器(Distortion)
在讲了这么多频域相关的数学后,是时候来点轻松些的内容了。
响度那一节当中我们提到过,摇滚乐会利用削波失真营造特殊的音响效果。当波形振幅太大,超出了系统的记录范围,就会导致波形被削顶,其频域成分也就会改变。如下图。

被削波后的波形会产生数量较多的谐波,使其音色发生变化。
由于模拟设备的特性,削波还分为软削波和硬削波。数字音频处理中最容易实现的是硬削波。
压缩器(Compressor)
压缩器类似于一个自动的音量推子,当音量超过设定的阈值后,自动以一定的比例减小音量,当音量低于阈值后再把音量复原。压缩器可以降低音乐的动态范围,让低音量的细节声音也能被听清,同时让音量过高的部分降低音量,保护耳朵和音响。

如图,可以看到音频在音量突然变大后,压缩器开始启动并将音频音量以预定压缩比压小;在音频音量减小之后,压缩器停止压缩,释放音量。启动时间和释放时间一般称作attack和release。
代码实现上,在检测到音频振幅超出预定范围后,将音频按预定压缩比降低音量即可。
压缩器对于响度差异大,声音忽大忽小的音频特别有用,比如VOCALOID编辑器直出的洛天依v3/v4萌干音。
限制器(Limiter)
在处理音频时,大部分时候我们不需要失真效果。限制器可以将音频振幅减小到指定范围内,同时保持波形不变(不削波)。
限制器的实质是一种启动时间极短,压缩比无限大的压缩器。与压缩器总以固定压缩比减小音量不同,限制器没有固定压缩比,会减小音量直到音量小于阈值为止。
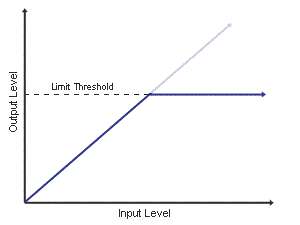
在音乐制作中常用限制器配合增益来最大化响度。但如果为了响度一味的压音频,就会损失过多动态范围,听起来很塑料。
延迟器(Delay)
延迟器会创造出一个不断衰减的“回声”效果。这里有一个示例(注意45秒之后“色彩”两个字的回音)。
延迟间隔一般和歌曲BPM节拍是同步的。这里设延迟时间为T,每一次延迟之间强度比都是a,则有:
$Y[t]=X[t]+a*Y[t-T]$
和数字滤波器同理,只需要用一个循环结构迭代即可。时间复杂度为$O(n)$。
由于和数字滤波器采用了相同的迭代结构,迭代过程中还可以先输出,再给信号进行滤波,这样每回音一次回音都会被滤波器作用,产生特定频段(常常是低频)不断衰减/增强的效果。
也有一些效果更复杂的延迟器,比如回音在左右声道不断跳动的Ping pong延迟,每次回声都反相处理,加入调制模块(Modulation)实现动态延迟时间等。实现起来并不复杂,这里暂不做讨论。
混响器(Reverb)
真实世界中,音频在空间中传播时会被不断反射。大多数时候反射声在原声发出后很短时间内到达人耳,因此人耳会将其认为是一个声音。混响会使声音变得跟浑厚,具有空间感,更自然。
人耳会先听到几个早期反射声,随后反射声和反射声的反射声在空间里不断传播,衰减,逐渐混合在一起。
与回声间隔固定的延迟器不同,混响是自然空间中的反射,因此无法用简单的迭代来模拟。大多数数字混响效果器会使用冲激响应函数的卷积(convolution)。
冲激函数(impulse function)在物理学上也被称作狄拉克函数。冲激函数的表达式如下:

此外,冲激函数的积分为1:

在数字信号处理中,狄拉克函数的对应离散函数被称作单位冲激函数(unit impulse function)。其定义如下:

冲激函数相当于一个极短的,强度为1的脉冲。冲激响应函数是系统对这个脉冲的响应,比如这样的:

响应函数可以理解为脉冲在发出后,在空间内不断反射,并在随后的时间中不断到达人耳。输入信号可以看做由一系列不同强度的冲激组成。信号$f(t)$经过冲激响应函数为$g(t)$的系统后,$t$时刻的输出相当于$\sum_{n=0}^{\infty} f(t-n)g(n)$。
举例来说,$t$时刻的信号相当于$f(t)*g(0)$(这个信号在系统里经过了0时刻)加上$f(t-1)*g(1)$($t-1$时的信号经过了1时刻)加上$f(t-2)*g(2)$…等等。引用知乎@palet的图示来解释,如图:
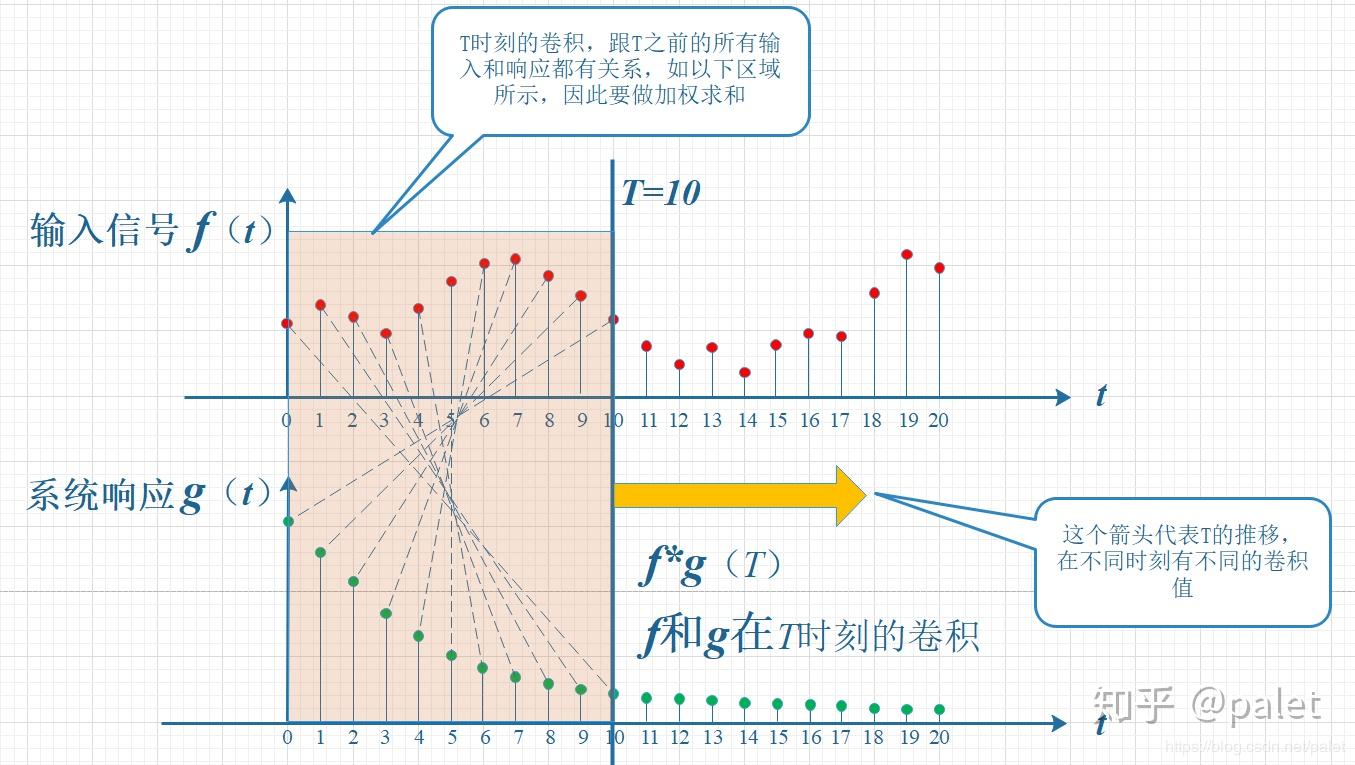
反转平移,得到卷积表达式:
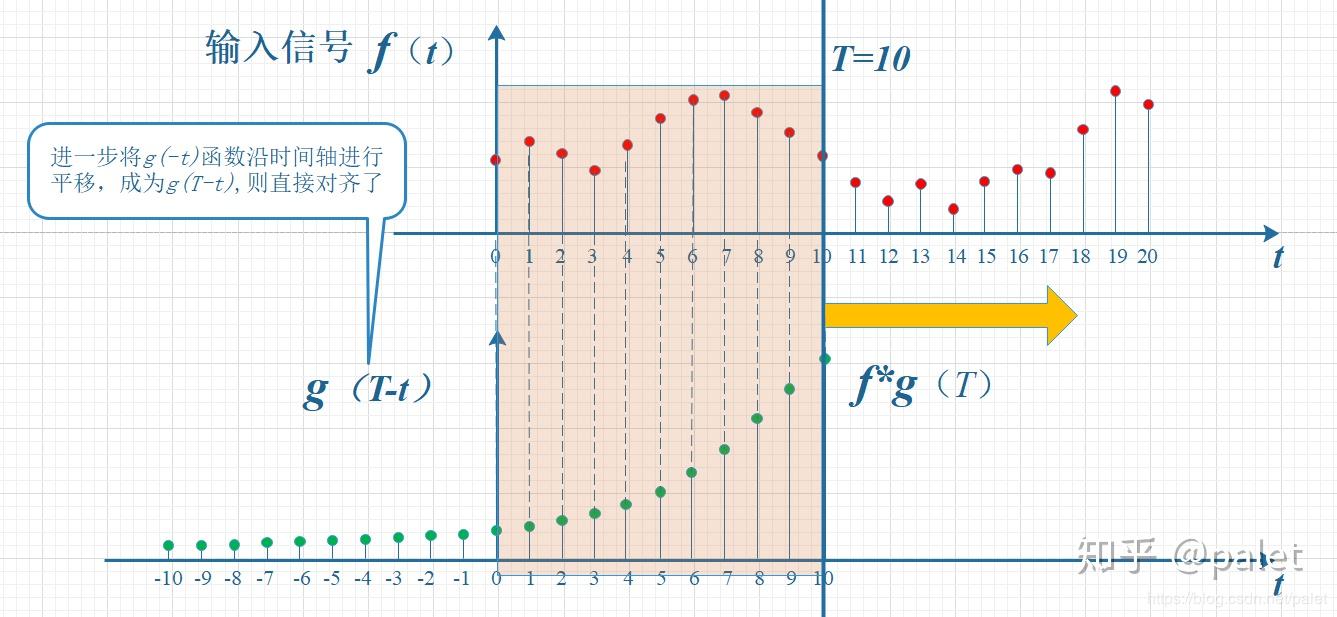
$(f*g)(n)=\sum_{\tau=-\infty }^{\infty}f(\tau)g(n-\tau)$
实际操作中采样长度和脉冲响应函数都是有限长的。而且混响在一段时间以后基本衰减到人耳听不见的范围内,考虑到计算开销可以适当缩减卷积大小。
参考文献
