In this section, we will be discussing some applications of Fourier transform in digital audio.

Unfortunately, I don’t have enough time to implement every content in this article by code myself …… so the article is basically a theory-based discussion. Please understand if there are any errors and omissions. This article will also cover a little bit of quantum mechanics. Yes, I listen to a song, mix a sound, and that involves quantum mechanics.

Fast Fourier Transform (FFT)

We have to take the time complexity into account when implementing the Discrete Fourier Transform (DFT) in a computer.

According to the DFT formula in the previous section, it is easy to see that the process of finding the weights (amplitudes) for each frequency requires $N$ complex multiplications and $(N-1)$ complex additions. When solving for $N$ frequencies, the time complexity will be $O (n^2)$.

An $O(n^2)$ algorithm will definitely be a problem under a sample rate of 40kHz. We need some optimizations.

To make things easier, we assume the sample size is a power of 2. First, in order to simplify the formula, let $W_N=e^{-j2\pi /N}$. And the DFT formula is therefore

$X[k]=\sum_{n=0}^{N-1}x[n]W_N^k$

If you don’t get this, remeber the real part of $W_N^k$ is $\cos 2\pi kn/N$, imaginary part of it is $i\sin 2\pi kn/N$. $W_N$ has the following properties:

• Periodicity. $W_N^k=W_N^{k+tN}$. Similar to $\sin 2\pi x=\sin 2\pi (x+k)$.
• Symmetry. $W_N^{k+N/2}=-W_N^k$. Same as $\sin x=-\sin (x+\pi)$.
• Scalability. $W_N^k=W_{N/2}^{k/2}$, because they are obviously the same when you simplify them.

We start from spliting the sample sequence into odd terms and even terms. Let $X [k]=G [k]+H [k]$. $G[k]$ are the even terms$G [k]=\sum_{n is even}^{N-2} x [n] W_N^{kn}$. $H[k]$ are the odd terms $H [k]=\sum_{n is odd}^{N-1} x [n] W_N^{kn}$.

What is the relationship between $X [k+N/2]$ and $X[k]$?

$X [k+N/2]=\sum_{n is even}^{N-2} x [n] W_N^{nk+nN/2}$. $n/2$ is always an integer since $n$ is even.

Using its periodicity:

$\sum_{n is even}^{N-2} x [n] W_N^{nk+nN/2}=\sum_{n is even}^{N-2} x [n] W_N^nk=G [k]$

Same for the odd terms:

$X [k+N/2]=\sum_{n is odd}^{N-1} x [n] W_N^{nk+nN/2}$

$=\sum_{n is odd}^{N-1} x [n] W_N^{nk+(n-1) N/2+N/2}$

$(n-1)/2$is always an integer since $n$ is odd. Again, using its periodicity:

$=\sum_{n is odd}^{N-1} x [n] W_N^{nk+N/2}$

Using its symmetric property:

$=-\sum_{n is odd}^{N-1} x [n] W_N^{nk}=-H [k]$

Therefore:

$X[k+N/2]=G[k+N/2]+H[k+N/2]=G[k]-H[k]$

Which means, we only need to calculate the first half of the sequance. The result for the first half can be reused to get the other half. We halved the computation!

Using its scalabilitym, we can also rewrite $G[k]$ and $H[k]$：

Even terms:

$G[k]=\sum_{n=0}^{N/2-1}x[2n]W_N^{2kn}=\sum_{n=0}^{N/2-1}x[2n]W_{N/2}^{kn}$

Odd terms:

$G[k]=\sum_{n=0}^{N/2-1}x[2n+1]W_N^{(2n+1)k}$

$=W_N^k\sum_{n=0}^{N/2-1}x[2n+1]W_N^{2nk}$

$=W_N^k\sum_{n=0}^{N/2-1}x[2n+1]W_{N/2}^{nk}$

Do you see that? The calculation of odd terms and even terms are standard DFTs whose computation can be halved again using the same method.

Now we have lowered the time complexity into $O(n \log n)$. It is possible to implement FFT in code using recursion. Of course, DFT is a rather performance-sensitive application, and the large number of recursive function calls affects the speed, so the code implementation is often expanded into non-recursive methods such as butterfly diagrams. Such a DFT is called a Fast Fourier Transform (FFT).

Short-time Fourier transform (STFT)

There is a small problem with the Fourier transform: it deals with a whole segment of samples, and the resulting frequency domain is the average of a whole segment of samples. This is obviously not the case in real audio: every second there are different tones that sound and stop sounding, and the sound is constantly getting louder and smaller. The Fourier transform can only find a fixed overall frequency domain map, but the real sound has a constantly changing frequency domain.

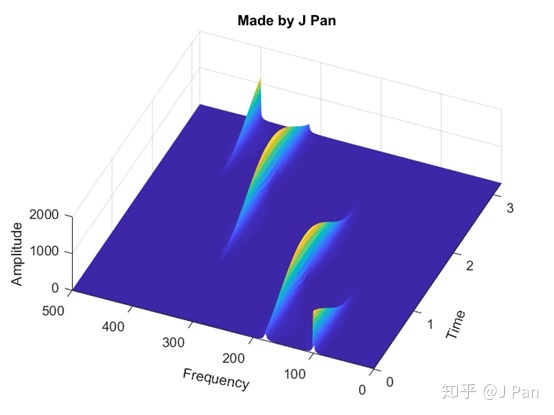
Short-time Fourier Transform (STFT) assumes that the frequency domain of the audio is constant over a short period of time. STFT cuts the audio into frames and performs a separate FFT on each frame to obtain a frequency-time-varying graph with the frame length as the time resolution. The time-frequency diagram is also called a spectrogram, which looks like this:

Since the frame size is not necessarily an exact multiple of the period, spectrum leakage can occur at both ends of the frame, resulting in a spectrogram that contains frequencies that should not be there. The solution is usually to add a window to the framse, i.e., to multiply it by a window function. Commonly used window functions include rectangular windows, Hann windows and Hamming windows. For example, if we have a signal like this:

Using the window function below:

This will be the result.

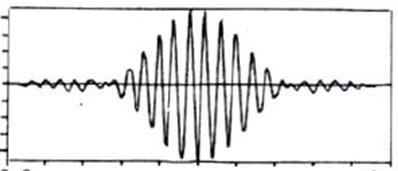
Since the signal amplitude near the ends of the frames becomes relatively small after the application of the window, it is often ignored in the processing. To solve this issue, we often make the frames overlap to ensure that the algorithm fully analyzed all frequencies in the signal.

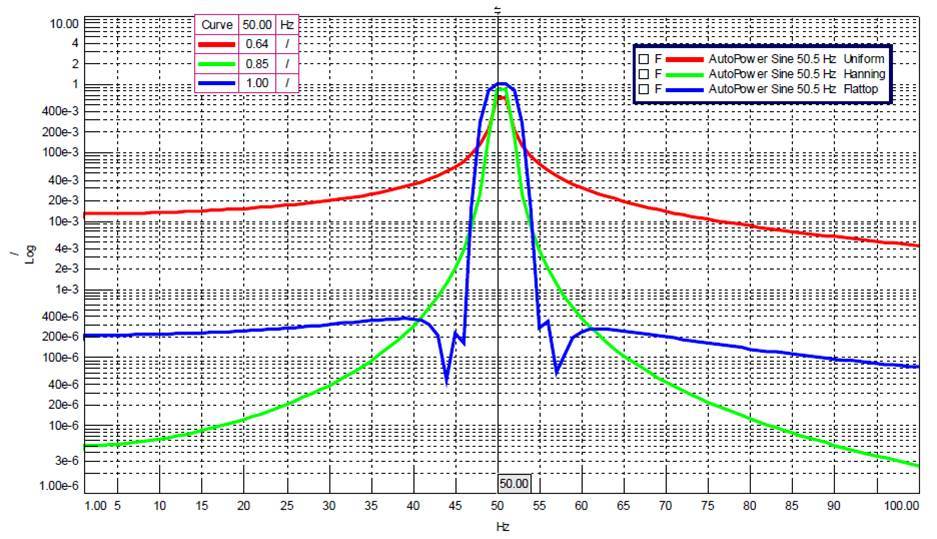
Different windows have different spectral characteristics. The application is generally based on the need for frequency accuracy and amplitude accuracy to select the window. A rectangular window (red), a Hanning window (green) and a flat-top window (blue) are applied to the signal at 50.5 Hz (frequency resolution of 1 Hz), displaying the amplitude in logarithmic scale. The result is below:

Uncertainty principle

For Fourier transform in the analysis of periodic functions, taking into account the truncation effect and other effects, the larger the sampling frame of the analysis, the higher the accuracy of the analyzed spectrum. However, this is contradictory to our time-frequency analysis; the longer the individual samples analyzed, the lower the time resolution.

This principle states that “ One cannot know the exact time-frequency representation of a signal, i.e., one cannot know what spectral components exist at what instances of times.

Cited from: Eceforum

For instance, for the following sinewave signal:

The time-frequency analysis with a smaller window has a high time resolution and a low frequency resolution.

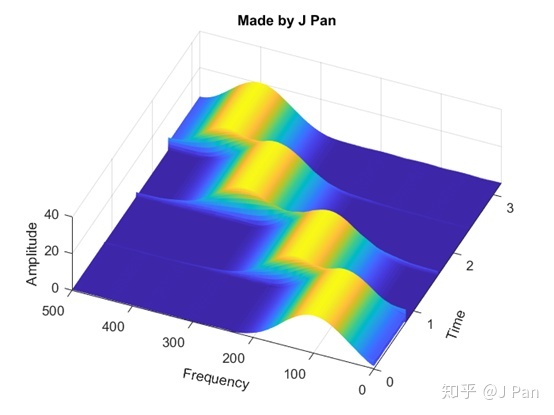
When using a larger window for time-frequency analysis, the frequency resolution becomes does become higher, but the time resolution becomes worse.

Remember the de Broglie wave in quantum mechanics? According to the basic assumptions of quantum mechanics, the wave function describes the probability of a particle appearing everywhere in space, i.e., the particle position is a wave on space. Also, the momentum of the particle is proportional to the frequency of the wave.

The problem arises when we use the Fourier transform to solve from one to the other: the momentum wave function and the position wave function can be obtained as Fourier transforms of each other (conjugate), just like our time domain signals and its frequency domain. Increasing the resolution of one inevitably leads to a decrease in the resolution of the other.

The Heisenberg uncertainty principle is actually an example of the uncertainty principle in the Fourier transform.

Sometimes, in order to make a reasonable trade-off between time resolution and frequency resolution, the transform will apply different window sizes to different frequencies to achieve the best possible results. In addition, there are also wavelet transform and other improvement methods. We will not talk about them here.