在上一篇中,我们讨论了声音在自然界中的存在形式和乐理的基础。这一篇将讨论音频的数字化存储的相关概念。
在数字化时代到来之前,音频一般使用磁带、唱片等形式存储模拟信号。模拟信号容易失真(当然也有人很喜欢这种失真,称之为“模拟味儿”),难以长距离传输,最关键的是:难以被计算机读取和处理。在数字时代来临后,音频转向了以采样为基础的数字存储。
采样
声音的模拟波形可以看作一个连续的时间-振幅曲线。采样(sampling)的过程将这个连续的曲线转换为离散的时间-振幅序列。通俗一点讲,采样就是在曲线上以固定间隔打点。
采样率(sample rate)是每秒采样的数量,常用值包括44100Hz、48000Hz等。根据香农采样定理,要想不失真的恢复模拟信号,采样率需要大于等于信号频率的两倍。人耳的听力范围一般在20-20000Hz间。但模拟音频因为噪声、声音干涉等原因可能会包含超过20000Hz的信号,为了避免可能的失真,采样率经常高于40000Hz。
采样率小于被采样信号频率的两倍时,还原的信号会出错。图中红线为被采样信号,蓝线为还原出的错误信号:

采样精度,或位深度(bit depth)指计算机用来存储每个声音样本的位数。位数越多,采样值越精确,声音还原的质量越高。下图描述了将模拟波形采样为4bit数字信号的过程:

8bit整数深度可以记录256级的振幅,16bit整数可以记录65536级。大多数情况下16bit已经足够使用,追求更高精度还有24bit整数和32bit浮点等可选项。采样深度越高,采样过程中四舍五入到最近值时产生的量化误差就越小。信号-量化噪音比的计算公式如下:
$SQNR = 20\log_{10}{2^Q } \approx 6.02Q dB$
16bit采样深度的信噪比大约为96.3dB。作为对比,大部分音乐的动态范围在40dB以内。
当采样深度较低时或输入信号太弱时,输入信号可能会一直被舍入到0导致无法记录。采样时可以加入一个较低的噪声,称为抖动(dithering)来避免此现象。
在Cubase中放大波形可以看到采样点。以下是《Walking seasons》的左声道放大后某处:

人耳听到的是立体声(stereo),通过左右耳的时间差、音量差可以感知声源的空间位置。最常用的立体声包含了左右耳两个声道(channel)。
存储格式
采样后音频最简单的存储方法是把所有采样点顺序记录。这种记录方式被称为脉冲编码调制(Pulse code modulation,或PCM)。PCM是无压缩的,保存的音频没有任何质量损失,代价是体积相对较大。采用这种编码方法的文件格式有小端序的.wav和大端序的.aiff。
一个440Hz的正弦波以1000Hz采样率采样时,振幅序列a[]为{0,0.426,0.771,0.969,0.982,0.808,0.481,0.062,-0.369,…} 对于第n个采样点,振幅可以用以下的函数描述:$f(x)=\sin ( \frac{440x}{1000})$。采样过程相当于根据这个函数生成离散序列。
无压缩的PCM体积实在是太大了。以16bit(2Byte)采样深度、44100Hz采样率的双声道音频计算,一分钟的音频需要整整$ 2\times44100\times60\times2$字节存储,或者说差不多10MB的空间,一首四分半的歌就有将近50MB大小——有没有办法减小体积呢?
作为一种无损压缩的编码方式,FLAC格式将PCM采样数据切割成一个个数据块,再针对数据块进行压缩。这种压缩和zip、rar等文件压缩格式类似,可以完整还原出压缩前的波形数据,因此音质和.wav没有区别。flac的缺点是对不同音频压缩率不同,且文件仍相对较大——体积大约是wav的一半。还能不能再小?
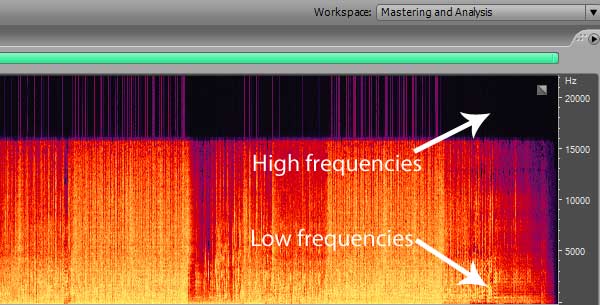
为了进一步减小音频体积以满足传输需求,MPEG-layer III格式,简称MP3,于1991年被发明。MP3采用了有损的压缩方式,利用人耳对中低频敏感,高频不敏感的特性,对不同频段施加不同的有损压缩。这种压缩方式能够达到10:1以上的压缩比,极大方便了音频的传输。
注意看下方的频谱图。16kHz以上的高频部分几乎都被切掉了:
响度
声音的响度单位是分贝dB(Decibel),即十分之一贝尔。由于人耳的听觉特性,声功率和人主观感受的响度不是线性关系,而是对数关系。
在描述声能等功率量时,贝尔表示被测值是参考值的十的多少次方倍,10分贝(1贝尔)为$10^1$倍,n分贝为$10^\frac{n}{10}$倍。
此时分贝的计算公式为 $L_{dB}=10\log_{10}{(\frac{P_1}{P_0})}$。
当描述功率密度等场量时,贝尔描述的是被测量与参考值的平方之比。这是由于绝大多数场,包括引力场、电磁场以及声场,在传播时遵循平方反比定律——场强和场源距离的平方成反比。
此时分贝的计算公式为$L_{dB}=10\log_{10}{(\frac{A_1^2}{A_0^2})}$。
利用对数的性质,上述公式可写成:
$L_{dB}=20\log_{10}{(\frac{A_1}{A_0})}$。
在日常生活中衡量声音响度时,一般采用人耳的听觉阈值作为参考值。现实中人耳对于不同频率的声音敏感度不同。以下为ISO226中的响度-频率图:

在数字音频中,一般把采样值的最大范围作为参考值。此时单位为dBFS,就是dB full scale的意思。声压/幅值使用场量公式,给音频信号添加一个-20dBFS的增益(gain)时,其信号幅值减少到原来的十分之一。
PCM中增益x dB后,采样值与原采样值的关系为:
$A=10^{x/20}A_0$
需要注意的是,当信号幅度超出数字信号系统能够记录的上限时,无法记录的部分会被舍弃导致削波失真(distortion)。在模拟系统中,由于幅值是由电压等表示的,仍有一定余地应对超出的幅值;但在绝大多数数字系统中,并没有这一余量。
出于一些原因,摇滚乐爱好者觉得这种失真的噪声感很爽。由此诞生了许多电吉他效果器——先疯狂加音量产生失真,再把失真声音的音量降下来,好保护音箱。
