现在我们已经学会了二进制是什么,以及布尔逻辑变量的基本操作了。例如如何把两个布尔值进行逻辑运算:与运算,或运算和非运算。请务必熟练掌握Minecraft中这些逻辑门的搭建方法,因为从这一章开始我们将会大量用到它们。
这些逻辑门就像是乐高砖块,有了它们,我们就可以实现更复杂的功能。比如说,把两个数相加。
加法器
两个一位二进制数相加可能会产生四种结果。
| 加数1 | 加数2 | 结果 |
| 0 | 0 | 00 |
| 0 | 1 | 01 |
| 1 | 0 | 01 |
| 1 | 1 | 10 |
结果是两位二进制数,也就意味着我们需要两个输出来表示每一位。个位的输出事实上相当于对两个数做异或运算:如果两个数相同,例如都是0或者都是1,个位的结果是0。只有当两个数不同,其中一个为1另一个为0的时候,个位的结果才是1。只要在输入后面放一个异或门,就得到了个位的结果。
观察结果的十位(也就是进位)。只有当两个数都是1时,相加结果才是10。这也正是与门的工作逻辑。在输入后面放一个与门,我们就得到了结果的十位。现在把与门和刚刚的异或门放到一起,我们就得到了一个能计算一位数二进制加法的半加器。
只能算一位数的计算器大概没什么用。要想计算更多位数我们需要能处理进位的全加器。与半加器不同,全加器在相加两个输出后,会把结果和进位再次相加。真值表如下:
| 输入A | 输入B | 进位 | 有无进位产生 | 结果个位 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全加器其实就是两个半加器首尾相连。第一个半加器负责把头两个输入相加,第二个半加器负责将结果和进位相加,再用一个或门处理它们产生的进位。我们可以在Minecraft中这样搭建一个半加器:

在图中左侧的铁块为半加器的两个输入,蓝色部分为异或门,其信号将输出至前方的红石灯上。黄色部分为一个产生进位的与门,其结果将输出到图中青色笔迹标注的方块上。
将两个半加器构成全加器,并将这一位的进位结果传输给下一位全加器,我们就能够计算多位加法了。这种逐级进位的加法器被称为行波进位加法器。
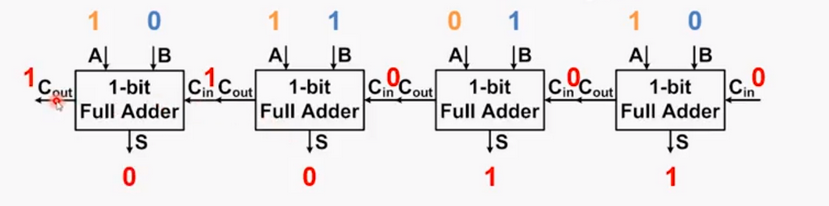
在Minecraft中,我们可以这样实现行波进位加法器:

注意观察图中的八位加法器是如何实现从左到右的进位的。从最右边开始每个全加器中的第一个半加器(蓝色)将两个输入相加并传递给第二个半加器(粉色)。第二个半加器将第一个全加器的输入与上一位的进位(黄色)相加得到最终的结果。两个半加器产生的进位通过黄色线汇总并传递给下一个全加器。
最后一个全加器产生的进位会因为超出八位被直接丢弃掉,此时全加器将输出错误的结果。我们管这样的情况叫做溢出。
在溢出时,计算结果比实际结果少了一位,数值上少了1 0000 0000。记住这一点,一会儿要用到!
减法和负数
计算减法的一种可行方法是把像构建加法器那样构建减法器。写出每一位的计算规则和借位规则然后做一个全减器出来。不过大多数情况下使用的是另一种方法:计算A-B,实际上就是计算A+(-B),即A加上B的负数。我们只需要用负数表示B就可以了。
直接用二进制把数写出来的表示方式叫做原码,而计算机使用一种叫补码的东西表示负数。根据补码的规则,八位带符号整数中第一位将用来表示正负。正数为0,负数为1。正数的补码就是它自身(即原码),负数的补码是其绝对值的原码逐位取反再加上1。
例如对于-1的补码,我们可以先把其绝对值的原码写出来:0000 0001。逐位取反得到其反码1111 1110,取反后的结果加上1就得到了它的补码1111 1111。
让我们试着做一下加法!例如2+(-1)。2的二进制值补码就是它自身,也就是0000 0010。-1的补码是1111 1111。
0000 0010 + 1111 1111 = 1 0000 0001。注意我们的数只有8位,因此超出八位的部分都被丢弃掉了。结果保留最后八位是0000 0001,也就是1。
2-1=1,结果正确。但是为什么会这样?
在我们的计算方式中,由于超出8位的部分会被丢弃,因此1111 1111再往后加一就又会回到0000 0000,就像是钟表上时针走过12之后又会回到1。补码相当于把所有负数都加上1 0000 0000——这样就能得到一个正数用于计算。而加上去的1 0000 0000会因为溢出在计算时被丢弃掉。就好像在钟表表盘上7点往后8个小时是7+8=15,我们丢弃了12,15-12=3。
二进制的乘法和除法也用到了非常巧妙的方法来计算。如果感兴趣的话,可以查找资料学习一下。
寄存器
在进行加减法计算后,我们需要一个草稿纸一样的存储空间来存放计算结果。寄存器可以存放一个数,并在需要的时候进行读取。
和以往一样,我们先学习只有一位时的情况。Minecraft中红石中继器的一个特性允许我们方便的保存当前状态:

当红石中继器被另一个红石中继器从侧面充能后,它就会“锁住”。在被锁住的状态下,不论输入的信号如何变化,其输出信号都不会改变。
因此,只需要放置一行的中继器,再用一根红石线统一控制锁住/解锁,就可以保存一个二进制数字。
内存
对于真正的计算机系统来说,单个八位寄存器一个字节的存储空间显然是远远不够的。两个寄存器也不够。能够实现简单功能的单片机,例如Arduino uno,往往有着数千字节大小的内存。这些内存空间用内存地址进行编号,我们可以通过内存地址来访问内存的指定位置。
内存模块由非常多的内存单元构成。它们共用输入输出端口,内存模块会根据地址选择具体的内存单元进行读写操作。
让我们造一个64bit的内存。如果只是将64个寄存器排在一起,我们的内存模块将会不切实际的长。所以与其排在一起,我们用一个8×8的矩阵来代替。首先我们做出这样的可堆叠单元:


这样的模块可以在横向和纵向上进行堆叠。黄色的横线是数据的读取和写入线。蓝色的为一根从底部向上统一开关的写入使能线。矩阵中的单元使用两根线进行定位:绿色行选中和橙色列选中。对于地址第7行2列来说,内存模块将会打开第七行的行选中线和第二行的列选中线。内存模块的大小是64,也就是6位宽度的地址。地址中的1-3位代表列,4-6位代表行。
当行选中和列选中同时激活时,内存单元会在数据输出线上输出存储的数据状态(高或者低)。如果此时在写入使能上给予一个脉冲,单元将会将红石中继器解锁再锁定,将存储值更新为数据输入线上的值。
将这样的模块像上垂直堆叠八个,我们就有了位宽为8的一个内存大模块:可以存储一个字节了!
将竖起来的“字节高塔”在平面上进行8×8的堆叠,我们就可以存储64个字节。最后记得将每一行的行选中和每一列的列选中串联起来,这样我们就可以选择几行几列了。
完成之后,这样的模块从底部看是这样的,可以看到一条条横向的列选中线:
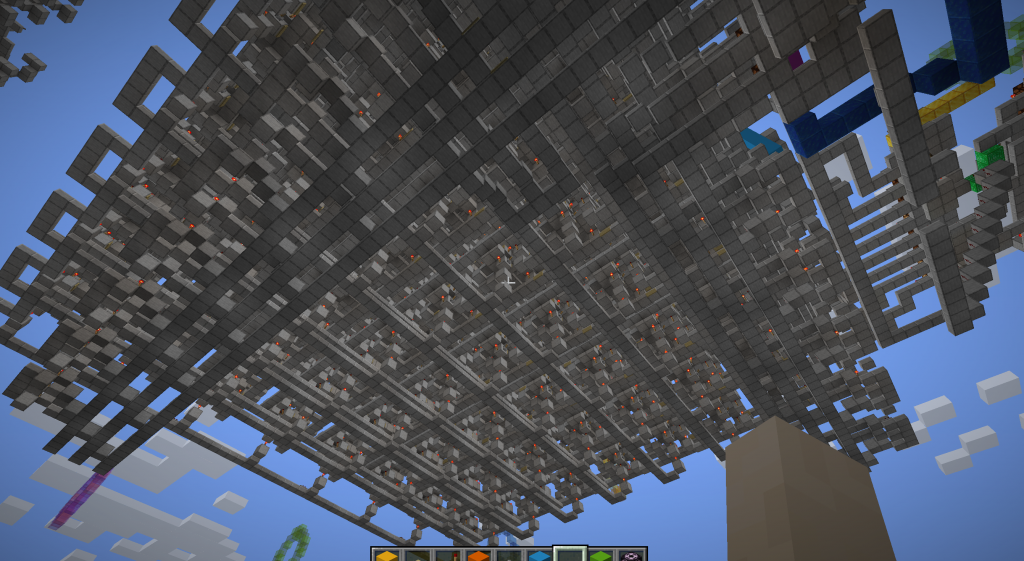

怎样根据二进制的序号点亮对应的地址线呢?隆重介绍——
多路复用器
先来考虑一个相对简单的问题:如何判断一个二进制值是不是110?
我们可以将这个问题转换为:如果给定三个输入,如何判断第一个输入是否是1,第二个输入是否是1,第三个输入是否是0?
可写出以下逻辑表达式:结果=(A是1吗?)与(B是1吗?)与(C是0吗?)
等同于:结果=A与B与(!C)。
这也就是Minecraft社区解密地图中常见的密码门的原理。当且仅当输入值是特定二进制数时,输出才是1。
让我们把它造出来。(下图的设计经过了一些简化,实际逻辑原理与上面提到的等同)

现在我们已经可以根据二进制数决定是否选中一行了。接下来只需要制作剩余的多路复用器并让它们共用输入就可以了。成品看起来就会像之前图片中内存底部的样子。
现在你已经拥有了一个可以工作的内存模块了!要想读取指定内存位置的值,我们只需要输入正确的地址,值就会被输出;要想改写指定位置的值,应该在数据输入端写好数据,在地址端写入要修改的地址;最后给写入使能线一个脉冲信号。
在下一章中,我们将学习如何将元件连接起来并高效的传输数据。

评论