Before the age of digitalization, audio was generally stored using analog signals in the form of tapes, records, etc. Analog signals were prone to distortion (some people, of course, loved such distortion and called it “analog flavor”), difficult to transmit over long distances, and most critically: difficult for computers to read and process. Today, audio is usually digital.

Sampling

The analog waveform of a sound is a continuous time-to-amplitude curve. The process of sampling converts this continuous curve into a discrete time-to-amplitude sequence. In more general terms, sampling means hitting points on the curve at fixed intervals.

The sample rate is the number of samples per second. It is usually 44100Hz or 48000Hz. According to Shannon’s sampling theorem, in order to recover an analog signal without distortion, the sample rate needs to be greater than or equal to twice the frequency of the signal. The hearing range of the human ear is generally between 20-20000Hz. However, analog audio may contain signals above 20,000Hz due to noise, sound interference, etc. To avoid possible distortion, the sampling rate is often higher than 40,000Hz.

Sample resolution, or bit depth, refers to the number of bits a computer uses to store each sound sample. The more bits, the more accurate the sample value and the higher the quality of the sound reproduction. The following diagram illustrates the process of sampling an analog waveform into a 4-bit digital signal.

The 8bit integer depth can record 256 levels of amplitude, and the 16bit integer can record 65536 levels. In most cases, 16bit is enough. People use 24bit or 36bit float for higher quality only. Quantization error is the error caused by rounding when sampling. The higher the sampling depth, the lower the quantization error. This is the formula of the signal-to-noise ratio:

$SQNR = 20\log_{10}{2^Q } \approx 6.02Q dB$

The SQNR for 16bit depth is around 96.3dB. For comparison, most music has a dynamic range of 40dB or less.

When the sampling depth is low or the input signal is too weak, the signal may disappear during the sampling process. By adding a low noise level, called dithering, during the sampling process, we can avoid such problem.

We can observe the samples by zoom-in the Cubase. The waveform below is from the song ‘Walking seasons’:

What we hear in real life by both of our ears is stereo sound, which have two channels. Our brain process signals from both ears to locate the source of sound.

Audio format

The simplest way to store audio after sampling is to record all samples in sequence. This recording method is called pulse code modulation (PCM), which is uncompressed and saves the audio without any loss of quality. However, PCM has a large file size.

WAV is a small end PCM format. AIFF is a big end PCM format.

When sampling a 440Hz sine wave, the amplitude sequence a[] is {0, 0.426, 0.771, 0.969, 0.982, 0.808, 0.481, 0.062, -0.369, …}. The amplitude of the n th sample is :

$f (x)=\sin ( \frac {440x}{1000})$

The sampling process is equivalent to generating a discrete sequence based on the continuous function of the wave.

The size of the uncompressed PCM format is just too big. For example, a dual-channel stereo with 16bit depth, 44100Hz sample rate has a size of $2\times44100\times60\times2$ bytes, or about 10 MB. Is there way to make it samller?

As a lossless compression encoding method, FLAC format cuts PCM samples into blocks of data and then compresses the blocks. The compression is similar to zip/rar files – which means the sound quality of FLAC is no different from WAV. The limitation of lossless compression is that the size is still too big after processing, around 50% of original WAV file.

The MPEG-layer III format, or MP3 for short, was invented in 1991 to further reduce the size of audio to meet transmission needs. MP3 takes advantage of the human ear’s sensitivity to low and medium frequencies and insensitivity to high frequencies. It applies different levels of lossy compressions to different frequency bands. This compression method can achieve a compression ratio of 10:1 or more, which greatly facilitates the transmission of digital audio.

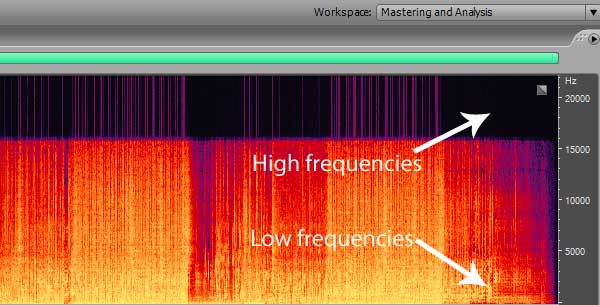
This is a spectrum graph of an mp3 file. You can see that the high frequency part above 16kHz has almost disappeared.

The unit of loudness of sound is decibel dB (Decibel), which is one tenth of a Bell. Due to the characteristics of the human ears, the sound power and the subjective human perception of loudness is not a linear relationship, but a logarithmic relationship.

When describing a power quantity such as sound energy, the decibel-to-multiplicity formula is $L_{dB}=10\log_{10}{(\frac {P_1}{P_0})}$.

When describing a field quantity such as power density, Bell describes the ratio of the square of the measured to the reference value. This is because most fields, including gravitational, electromagnetic, and acoustic fields, follow the inverse square law of propagation — the field strength is inversely proportional to the square of the distance from the field source.

The decibel-to-multiplicity formula is therefore $L_{dB}=10\log_{10}{(\frac {A_1^2}{A_0^2})}$.

Using the properties of logarithms, we can rewrite the equation:

$L_{dB}=20\log_{10}{(\frac{A_1}{A_0})}$

We usually use the auditory threshold of the human ear as the reference value when measuring sound loudness in real life. Human ears have different sensitivities to different frequencies of sound. Below is the loudness-frequency diagram in ISO 226.

In digital audio, the maximum range of sample values is generally used as the reference value. In this case, the unit is dBFS, which means dB full scale. Sound pressure / amplitude are field quantities that use the second equation. Adding a gain (gain) of -20dBFS to an audio signal reduces the signal amplitude to one-tenth of its original value.

The gain-to-multiplicity formula is:

$A=10^{x/20}A_0$

Clipping

It is important to note that when the signal amplitude exceeds the upper limit of a digital signal system, the portion that cannot be recorded is discarded resulting in clipping distortion (distortion). In analog systems, since the amplitude is represented by voltages, etc., there is still some margin to cope with the exceeded amplitude; however, in the vast majority of digital systems, there is no such margin.

For some reason, rock music lovers find this distorted noise feel cool. This has led to the birth of many electric guitar effects — first adding volume like crazy to create distortion, then lowering the volume of the distorted sound so as to protect the amp.